Prognozowanie w przedsiębiorstwie

Metody oparte na modelach szeregu czasowego

Główną cechą metod prognozowania opartych na modelach szeregu czasowego zmiennej prognozowanej jest budowanie prognoz na podstawie prawidłowości zaobserwowanych w dotychczasowym rozwoju prognozowanego zjawiska, bez wnikania w przyczyny ich występowania. Użycie tych metod jest jednak zasadne tylko wtedy, gdy prognozowane zjawisko charakteryzuje się dużą inercją. Konstruując prognozę, korzysta się wówczas z zasady status quo, tzn. przyjmuje się, że w okresie, na który jest budowana prognoza, na prognozowane zjawisko będą oddziaływały te same czynniki otoczenia przedsiębiorstwa i w taki sam sposób jak dotychczas, a realizowana strategia nie ulegnie zmianie. Metody należące do tej grupy są więc przydatne przede wszystkim do sporządzania prognoz krótkookresowych. Przetworzenie informacji o przeszłości w procesie prognozowania na podstawie szeregu czasowego następuje przez budowę odpowiedniego (do składowych szeregu) modelu formalnego, z kolei przejście od informacji przetworzonej do prognozy – przez wybór reguły prognozowania, którą najczęściej jest reguła podstawowa lub reguła podstawowa z poprawką.

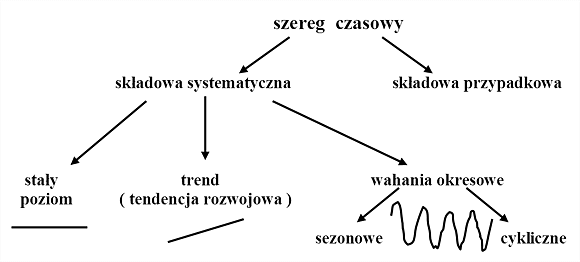
W szeregach czasowych wyróżnia się składową systematyczną, będącą efektem oddziaływań przyczyn głównych na zmienną prognozowaną, oraz składową przypadkową, zwaną także składnikiem losowym lub wahaniami przypadkowymi, będącą efektem oddziaływań przyczyn ubocznych. Składowa systematyczna (więcej 11)

Rys. Składowe szeregu czasowego 

występuje w postaci różnych prawidłowości w rozwoju prognozowanego zjawiska: stałego poziomu zmiennej prognozowanej, trendu (tendencji rozwojowej), składowej okresowej (wahań sezonowych i cyklicznych). więcej 12

Stały (przeciętny) poziom prognozowanej zmiennej występuje wówczas, gdy w szeregu czasowym nie występuje trend ani wahania okresowe, wartości zaś prognozowanej zmiennej oscylują wokół pewnego (stałego) poziomu.

Trend, będący długookresową skłonnością do jednokierunkowych zmian (wzrostu lub spadku) wartości prognozowanej zmiennej, jest efektem działania stałego zestawu czynników, takich jak np. w przypadku przedsiębiorstwa – liczba potencjalnych klientów, ich dochody, preferencje, ceny surowców czy konkurenci. Przejawia się w postaci rosnących (trend wzrostowy) lub malejących (trend spadkowy) wartości średniej arytmetycznej zmiennej prognozowanej. Trend może być wyznaczany, gdy się dysponuje długim szeregiem czasowym prognozowanej zmiennej.

Wahania cykliczne występują w postaci długookresowych, rytmicznych wahań wartości zmiennej wokół trendu lub stałego (przeciętnego) poziomu tej zmiennej. W przedsiębiorstwie mogą być związane z cyklem koniunkturalnym gospodarki oraz z cyklem rozwoju populacji nabywców produktów przedsiębiorstwa, determinowanym występowaniem niżów i wyżów demograficznych.

Wahania sezonowe są wahaniami wartości obserwowanej zmiennej wokół trendu lub wokół stałego (przeciętnego) poziomu tej zmiennej. Powtarzają się w przedziale czasu, nie przekraczającym jednego roku. Są efektem zmian pór roku, przyjętej konwencji podziału roku na kwartały, miesiące itd. oraz zwyczajów związanych z tymi faktami (wyjazdy na urlopy latem, wzmożone zakupy w okresie świąt itp.).

Ponieważ w zależności m. in. od rodzaju tych prawidłowości dokonuje się wyboru metody prognozowania, przeprowadza się ich identyfikację.

Identyfikację postaci tych prawidłowości szeregu czasowego umożliwia m.in.:

• wykres danych prognostycznych,
• test parametryczny współczynnika korelacji Pearsona,
• test nieparametryczny Danielsa współczynnika korelacji rang Spearmana,
• funkcja autokorelacji,
• analiza wariancji. więcej 13

  Wzrokowa ocena sporządzonego wykresu danych prognostycznych umożliwia często wstępne określenie prawidłowości występujących w szeregu czasowym zmiennej prognozowanej (identyfikację składowych szeregu). Rezultaty tej oceny powinny być jednak zawsze potwierdzone metodami statystycznymi.

  Parametryczny test współczynnika korelacji Pearson’a oraz nieparametryczny test statystyczny Daniels’a przeznaczony jest przede wszystkim do wykrywania trendu liniowego, lecz często pozwala także na wykrycie trendu nieliniowego.

  Stosując do identyfikacji składowych szeregu czasowego funkcję autokorelacji przyjmuje się że:

  1. Duże i statystycznie istotne wartości współczynników autokorelacji pierwszych kilku rzędów oraz stopniowo malejące następnych rzędów wskazują na występowanie w szeregu czasowym trendu.
  2. Statystycznie istotne wartości współczynników autokorelacji rzędu równego liczbie faz cyklu sezonowego, np. rzędu 4 (dla danych kwartalnych) lub rzędu 12 (dla danych miesięcznych), wskazują na występowanie w szeregu czasowym wahań sezonowych.

  Do oceny istotności współczynników autokorelacji można użyć statystyki Boxa-Ljunga.

  Jednoczynnikowa analiza wariancji może być używana do identyfikacji występowania w szeregu czasowym wahań sezonowych. Dwuczynnikowa analiza wariancji bywa stosowana do identyfikacji w szeregu czasowym trendu i wahań sezonowych.

W przypadku występowania w szeregu czasowym trendu jako modeli używa się:

• różnego rodzaju analitycznych funkcji trendu (funkcji liniowej, potęgowej, wykładniczej, logarytmicznej, itd.) więcej 14

  Funkcja liniowa:
  

  Funkcja wykładnicza:
  

  Wielomian stopnia drugiego (parabola):
  

  Funkcja potęgowa:
  

  Funkcja logarytmiczna:
  

  Wielomian (parabola) odwrotnościowy:
  

  Funkcja liniowo-odwrotnościowa:
  

  Funkcja ilorazowa:
  

  Funkcja logistyczna:
  

• modeli wygładzania wykładniczego dla szeregów czasowych z trendem (liniowy model wygładzania wykładniczego, model wygładzania wykładniczego z trendem hiperbolicznym, itd.) więcej 15

  Liniowy model wygładzania wykładniczego Holta

  Do opisu trendu w modelu używa się wielomianu stopnia pierwszego (prostej). Równania tego modelu są następujące:

      F_t-1 = αy_t-1 + (1 - α)(F_t-2 + S_t-2)
  

  oraz

      S_t-1 = β(F_t-1 - F_t-2) + (1 - β)S_t-2
  

  gdzie:

      F_t-1 – wygładzona wartość zmiennej prognozowanej na moment/okres t – 1,
      S_t-1 – wygładzona wartość przyrostu trendu na moment/okres t – 1,
      α, β – parametry modelu o wartościach z przedziału [0; 1],

  zaś równanie prognozy na okres t > n ma następującą postać:

      y_t^* = F_n + (t - n)S_n

  gdzie:

      y_t^* – prognoza wyznaczona na moment/okres t,
      F_n – wygładzona wartość zmiennej prognozowanej na okres n,
      S_n – wygładzona wartość przyrostu trendu w okresie n,
      n – liczba wyrazów szeregu czasowego zmiennej prognozowanej.

Używając jako modelu prognostycznego analityczną funkcję trendu, prognozę punktową otrzymuje się poprzez podstawienie w miejsce zmiennej czasowej t numeru okresu na który jest budowana prognoza. Do oceny dopuszczalności prognozy używa się błędu ex ante.
więcej 16.

Bezwzględny błąd prognozy ex ante w przypadku liniowej funkcji trendu jest dany wzorem:

zaś względny błąd prognozy ex ante:

gdzie:

    s – odchylenie standardowe składnika resztowego modelu, określone wzorem:

   

     n – liczba wyrazów szeregu czasowego zmiennej

    – średnia wartość zmiennej czasowej w próbie, na podstawie której szacowano parametry modelu.

Można także wyznaczyć przedział prognozy. więcej 17

W praktyce przedział prognozy buduje się najczęściej symetrycznie wokół wartości oczekiwanej zmiennej prognozowanej E(Y_τ), tj. wyznaczonej z modelu na okres t prognozy y_τ^*:

    P(y_τ^* - uv_τ ≤ y_τ ≤ y_τ^* + uv_τ) = p

gdzie:

    u – współczynnik związany z wiarygodnością prognozy, rozkładem zmiennej prognozowanej
         oraz długością szeregu czasowego (u > 0),
    p – wiarygodność prognozy.  

Stosując modele wygładzania wykładniczego prognozę punktową otrzymuje się poprzez podstawienie w równaniu prognozy w miejsce zmiennej czasowej t numeru okresu na który jest budowana prognoza. Do oceny dopuszczalności prognozy używa się błędu ex post prognoz wcześniejszych. 

Jeśli w szeregu czasowym zmiennej prognozowanej występują wahania sezonowe do prognozowania używa się m. in.:

• metody wskaźników, więcej 19

  Jest jedną z prostszych i częściej używanych metod w analizie i prognozowaniu wahań sezonowych. Polega ona na budowie modelu prognostycznego w postaci funkcji trendu oraz wskaźników sezonowości dla poszczególnych faz cyklu. W zależności od rodzaju wahań sezonowych (bezwzględnie i względnie stałe) używa się modeli addytywnych lub multiplikatywnych. Do opisu kształtowania się badanego zjawiska używa w pierwszym przypadku modelu addytywnego:

      y_ti = Y_ti + s_i + ζ_t, t  = 1, 2, K, n; i =1, 2, K, r
  

  Z kolei w drugim, częściej występującym przypadku stosuje się model multi¬plikatywny:

      y_ti = Y_ti s_i ζ_t, t = 1, 2, K, n; i = 1, 2, K, r
  

  gdzie:

      y_ti – rzeczywista wielkość sprzedaży w okresie t w i-tej fazie cyklu,
      Y_ti – teoretyczna wielkość sprzedaży w okresie t w i-tej fazie cyklu, wyzna¬czona z modelu trendu,
      s_i – wskaźnik sezonowości dla i-tej fazy cyklu,
      ζ – składnik losowy,
      r – liczba faz cyklu.

• analizy harmonicznej, więcej 20

  Inną metodą badania zjawiska sezonowości w szeregach czasowych jest analiza harmoniczna, polegająca na budowie modelu w postaci sumy tzw. harmonik, tj. funkcji sinus i cosinus o danym okresie. Jeśli w szeregu czasowym zmiennej prognozowanej występują: stały poziom, wahania sezonowe i wahania przypadkowe, to wówczas zapis odpowiedniego modelu jest następujący:

  

  gdzie:

      i – numer harmoniki,
      α0, α_i, β_i – parametry

  W przypadku, gdy w szeregu czasowym zmiennej prognozowanej występuje trend, wahania sezonowe i przypadkowe można zastosować model:

  

  gdzie: f(t) – funkcja trendu.

• modeli wygładzania wykładniczego dla szeregów czasowych z wahaniami sezonowymi np. modelu wygładzania wykładniczego z trendem liniowym Wintersa. więcej 21

  Model Wintersa może być stosowany do prognozowania, gdy szereg czasowy zmiennej prognozowanej zawiera trend, wahania sezonowe oraz wahania przypadkowe. A oto równania addytywnej wersji modelu:

  

  oraz multiplikatywnej wersji modelu:

  

  gdzie:

      F_t-1 – ocena wartości zmiennej prognozowanej w okresie t - 1,
      S_t-1 – ocena przyrostu trendu w okresie t - 1,
      C_t-1 – ocena wskaźnika sezonowości dla okresu t - 1,
      r – liczba faz cyklu sezonowego,
      α, β, γ – parametry modelu z przedziału [0; 1].

  Równania prognozy na moment/okres t > n są następujące:

      y_t^* = F_n + S_n(t - n) + C_t-r 

  (dla wersji addytywnej modelu)

      y_t^* = (F_n + S_n(t - n))C_t-r 

  (dla wersji multiplikatywnej modelu),

  gdzie: y_t^* – prognoza wyznaczona na okres t,

Metody oparte na modelach ekonometrycznych

Główną cechą metod prognozowania opartych na modelach ekonometrycznych jest budowanie prognoz na podstawie prawidłowości zaobserwowanych pomiędzy prognozowanym zjawiskiem a innymi zjawiskami. Proces budowy modelu składa się z następujących etapów:

• wybór zmiennych objaśniających modelu charakteryzujących zjawiska wpływające na zjawisko prognozowane (elementy otoczenia oraz strategii przedsiębiorstwa), więcej 22

  Jednym z trudniejszych zagadnień związanych z budową modelu jest wybór zmiennych objaśniających. Powinien on zawsze wynikać z przyjętych przesłanek prognostycznych. Na ogół jednak na prognozowane zjawisko, np. na kształtowanie się wielkości sprzedaży może wpływać wiele czynników, związanych zarówno z otoczeniem marketingowym przedsiębiorstwa, jak i ze stosowaną przez przedsiębiorstwo strategią marketingową. Często wynika stąd konieczność ograniczenia ich liczby. Ograniczenie to ma na celu zapobieżenie wprowadzaniu do modelu zmiennych powtarzających informacje dostarczane przez inne zmienne oraz dostarczających informacji nieistotnych. Wiadomo także, że im większa jest różnica między liczbą obserwacji a liczbą zmiennych objaśniających, tym dokładniejsze uzyskuje się oceny estymowanych w trakcie budowy modelu wielkości. To zaś z kolei wpływa na jakość konstruowanych prognoz.

  Z formalnego punktu widzenia przy konstrukcji modelu prognostycznego zmienne objaśniające powinny być silnie powiązane przyczynowo-skutkowo lub symptomatycznie ze zmienną prognozowaną oraz nie powiązane (lub jedynie słabo) między sobą. Mocne powiązanie zmiennych objaśniających ze zmienną prognozowaną gwarantuje, że model będzie dobrze dopasowany do danych empirycznych, słabe zaś ich wzajemne powiązania – że nie będą powielały dostarczanych przez siebie informacji. Jest to istotne ze względu na wielkość błędu ex ante budowanej prognozy oraz ze względu na stosowanie metody najmniejszych kwadratów, najczęściej używanej do estymacji parametrów modelu.

• wybór postaci analitycznej modelu, więcej 23

  W etapie tym powinna zostać udzielona odpowiedź na pytanie, jaką postać analityczną nadać modelowi, by najlepiej odzwierciedlała związek łączący zmienną prognozowaną ze zmiennymi objaśniającymi. Prawidłowe wykonanie tego zadania nie jest łatwe, ponieważ nie ma w pełni obiektywnych i jednoznacznych procedur wyboru postaci modelu. Zadanie to jest też dodatkowo utrudnione, gdyż cel budowy modelu w naszym przypadku stanowi budowa prognoz. Model bowiem powinien niekiedy dobrze opisywać powiązania zmiennej prognozowanej i zmiennych objaśniających nie tylko dla wartości zaobserwowanych w próbie, na podstawie której jest budowany, ale także dla wartości zmiennych wykraczających poza dotychczasowy ich obszar zmienności.

  Wybierając postać analityczną modelu można korzystać z teorii dotyczących badanych zależności bądź z doświadczeń wynikających z wcześniej prowadzonych badań, z wniosków wypływających z analizy zebranych danych statystycznych (wykresów przebiegu zmiennej objaśnianej względem zmiennych objaśniających, testów statystycznych) oraz z intuicji. Model powinien mieć zawsze możliwie prostą postać analityczną. Łatwiej jest wówczas oszacować jego parametry oraz zastosować do budowy prognoz.

• estymacja parametrów modelu, więcej 24

  Estymacja parametrów modelu powinna być tak przeprowadzona, by jej rezultatem był model jak najlepiej dopasowany do danych empirycznych zmiennej prognozowanej. Najczęściej stosowaną metodą szacowania parametrów modeli liniowych oraz nieliniowych, sprowadzalnych do postaci liniowej, jest metoda najmniejszych kwadratów.

  Klasyczna metoda najmniejszych kwadratów może być stosowana do szacowania parametrów liniowych modeli ekonometrycznych oraz modeli nieliniowych, sprowadzalnych do postaci liniowej. Sposób przeprowadzenia transformacji modelu zależy od jego typu. Jeśli model jest nieliniowy jedynie względem zmiennych objaśniających, a jednocześnie liniowy względem parametrów strukturalnych, to wówczas wystarczy podstawić za funkcje zmiennych objaśniających pewne nowe wielkości.

• weryfikacja modelu, więcej 25

  Przed przystąpieniem do prognozowania oszacowany model należy poddać weryfikacji merytorycznej, polegającej na sprawdzeniu czy model jest zgodny z wiedzą na temat badanego zjawiska i zdrowym rozsądkiem, oraz weryfikacji statystycznej, polegającej na sprawdzeniu czy model spełnia postulaty sformułowane w teorii ekonometrii.

  Chodzi tutaj przede wszystkim o sprawdzenie:

  1. stopnia zgodności modelu z danymi empirycznymi,
  2. istotności ocen parametrów strukturalnych,
  3. rozkładu odchyleń losowych modelu,
  4. stabilności postaci analitycznej modelu i stabilności parametrów modelu.

  Jeśli się okaże, że uzyskane w trakcie weryfikacji modelu wyniki nasuwają pewne wątpliwości dotyczące poprawności modelu, to należy ten model poprawić. Przyczyny powodujące złą jakość modelu mogą być związane z wszystkimi poprzednimi etapami jego budowy, tj. doborem zmiennych modelu, doborem postaci modelu, metodą estymacji parametrów modelu. Zazwyczaj nie wiadomo, co jest przyczyną złej jakości modelu, często więc model poprawia się metodą kolejnych empirycznych przybliżeń.

• budowa prognozy. więcej 26

  Do budowy prognoz mogą być stosowane zarówno modele symptomatyczne, jak i przyczynowo-skutkowe. Na ogół zakłada się że:

  1. Występuje stabilność relacji wiążących zmienną prognozowaną ze zmiennymi objaśniającymi, oznaczająca, że postać oraz wartości parametrów modelu, wynikające z dotychczasowego oddziaływania zmiennych objaśniających na zmienną prognozowaną, będą także właściwe dla okresu, na który jest budowana prognoza. Ocena prawdziwości tego założenia może być dokonana przez weryfikację postaci i parametrów modelu wraz z napływem nowych danych .
  2. Rozkład składnika losowego nie zmienia się w czasie, co oznacza, że nie pojawią się w okresie prognozy nowe, ważne zmienne wpływające na zmienną prognozowaną, oddziaływanie zaś dotychczasowych nie zmieni się w czasie.
  3. Znane są wartości zmiennych objaśniających w okresie, do którego odnosi się budowana prognoza, lub w przypadku modelu ze zmiennymi opóźnionymi w okresie wcześniejszym, wynikającym z przyjętego w modelu opóźnienia.

  Konstrukcja prognozy punktowej polega na ekstrapolacji modelu przez podstawienie odpowiednich wartości za zmienne objaśniające.

Konstruowanie prognozy punktowej polega na podstawieniu do modelu odpowiednich wartości za zmienne objaśniające. Źródłem tych wartości mogą być dla zmiennych:

• decyzyjnych – decyzje Sejmu (na przykład stopa podatku CIT), rządu, przedsiębiorstwa (zmienne charakteryzujące jego strategię),
• niedecyzyjnych makroekonomicznych – istniejące prognozy lub założenia, które określają ich przyszłe wielkości (na przykład wskaźnik inflacji, stopa bezrobocia, wskaźnik koniunktury),
• niedecyzyjnych mikroekonomicznych – prognozy budowane przez przedsiębiorstwo,
• opóźnionych w czasie – ich rzeczywiste wartości (jeśli opóźnienie jest większe od horyzontu prognozy).

Za wartości zmiennych:

• zero-jedynkowych – przyjmuje się 0 lub 1,
• czasowych – numer okresu, na który jest wyznaczana prognoza.

Do oceny dopuszczalności zbudowanej prognozy używa się błędu ex ante. więcej 27

Do oceny dopuszczalności prognozy używa się bezwzględnego błędu ex ante:

gdzie:

    v_t – bezwzględny błąd prognozy ex ante,
    a_i – ocena parametru α_i modelu,
    x_i,t^*– wartość i-tej zmiennej objaśniającej modelu w okresie t,
    D²(a_i) – wariancja oceny parametru a_i,
    cov(a_i, a_j) – kowariancja ocen parametrów a_i i a_j,
    s² – ocena wariancji odchyleń losowych,
    m – liczba zmiennych objaśniających modelu bez zmiennej stojącej przy wyrazie wolnym.

Metody jakościowe

Jakościowe metody prognozowania opierają się na opiniach ekspertów, którymi są osoby zaproszone do udziału w badaniu ze względu na posiadaną wiedzę. Jeśli prognozy buduje się w przedsiębiorstwie, to ekspertami mogą być jego pracownicy, osoby z nim współpracujące albo osoby z zewnątrz. Podobnie jak prognozy budowane metodami ilościowymi, prognozy konstruowane przez ekspertów przyjmują zwykle postać prognoz punktowych (wyrażanych w postaci jednej wartości zmiennej prognozowanej), prognoz przedziałowych (wyrażanych w postaci przedziału liczbowego) lub prognoz wariantowych (wyrażanych w postaci różnych wartości zmiennej prognozowanej). Prognozy mogą być formułowane zarówno przez jednego eksperta, jak i przez grupę ekspertów – w tym drugim wypadku postępowanie prognostyczne opiera się na ogół na metodzie delfickiej lub burzy mózgów.

Prognozowanie sprzedaży dóbr konsumpcyjnych w przedsiębiorstwach najczęściej oparte jest na opiniach: osób bezpośrednio zajmujących się sprzedażą, więcej 28

Ten sposób budowy krótko-, a niekiedy też średniookresowych prognoz sprzedaży został oparty na najprostszej postaci metody delfickiej, polegającej na jednokrotnym badaniu ankietowym. Badanie to sprowadza się do szacowania przyszłej wielkości sprzedaży produktów przedsiębiorstwa przez: bezpośrednich sprzedawców, menedżerów ds. sprzedaży bądź przedstawicieli handlowych, którzy odgrywają rolę ekspertów w dziedzinie ustalania wielkości sprzedaży na terytorium ich działania. Prognoza sprzedaży dla całego przedsiębiorstwa jest tworzona przez agregację prognoz zbudowanych przez poszczególnych ekspertów.

kierownictwa przedsiębiorstwa więcej 29

Ta jedna z prostszych, a przy tym częściej stosowanych metod prognozowania sprzedaży w przedsiębiorstwie może być stosowana w przedsiębiorstwach o różnej działalności, zwykle jest jednak używana w przedsiębiorstwach usługowych oraz produkujących dobra konsumpcyjne. Prognozę uzyskuje się w wyniku dyskusji osób należących do kierownictwa przedsiębiorstwa, zebranych w jednym pomieszczeniu (burza mózgów). Przy stosowaniu tej metody dąży się do uzyskania jak największego zasobu informacji na dany temat. Dlatego też oprócz osób odpowiedzialnych za sprzedaż w dyskusji na ogół biorą udział także osoby odpowiedzialne za produkcję, zaopatrzenie, finanse i administrację. Często też w ramach wprowadzenia do dyskusji przedstawia się dane charakteryzujące przedsiębiorstwo oraz jego otoczenie marketingowe, które mogą być użyteczne przy budowie prognozy.

bądź ekspertów spoza przedsiębiorstwa. więcej 30

Prognoza sprzedaży przedsiębiorstwa może być zbudowana również na podstawie opinii uzyskanych od ekspertów spoza przedsiębiorstwa. Ekspertami mogą być m.in. dealerzy, dostawcy czy konsultanci marketingowi. Ich opinie mogą dotyczyć bądź wielkości przyszłej sprzedaży przedsiębiorstwa, bądź wielkości przyszłego popytu rynkowego na dany produkt. W tej drugiej sytuacji prognozę sprzedaży przedsiębiorstwa można uzyskać, mnożąc wielkość popytu rynkowego przez spodziewany udział przedsiębiorstwa w rynku. Zebranie opinii odbywa się zwykle w rozmaity sposób. Zgromadzeni eksperci mogą przez wymianę poglądów (metodą grupy dyskusyjnej) doprowadzić do powstania wspólnej prognozy. Mogą też indywidualnie dostarczać swoje prognozy, na których podstawie jest tworzona jedna wspólna prognoza. Inny sposób stanowi zastosowanie metody delfickiej, polegającej na zebraniu opinii od ekspertów, zweryfikowaniu uzyskanych odpowiedzi w przedsiębiorstwie i odbyciu ponownej rundy (rund) formułowania prognoz przez ekspertów. Ostateczną prognozę dla przedsiębiorstwa można budować w różny sposób, np. jako średnią arytmetyczną prostą ważoną, medianę bądź dominantę. Metoda jest często używana dla określenia długookresowych tendencji w popycie.

Do prognoz budowanych przez ekspertów mogą być przypisane prawdopodobieństwa subiektywne ich realizacji, które określają, jakie są, zdaniem eksperta, szanse na to, że wartość zmiennej prognozowanej w okresie prognozy będzie:

• równa określonej wartości zmiennej prognozowanej (prognoza punktowa),
• zawarta w określonym przedziale liczbowym (prognoza przedziałowa),
• równa danemu wariantowi prognozy (prognoza wariantowa).

Prawdopodobieństwo subiektywne jest określanym przez eksperta prawdopodobieństwem zajścia określonego zdarzenia. Jeśli prawdopodobieństwa te zostały przez eksperta określone, to – dla prognoz punktowych i przedziałowych – można ich użyć do oceny dopuszczalności (wiarygodności) prognoz. Dla prognoz wariantowych ekspert może sformułować prognozę w postaci wszystkich lub wybranych, możliwych wartości zmiennej prognozowanej i ewentualnie przypisanych do nich prawdopodobieństw subiektywnych realizacji. Ostateczną prognozę można wówczas określić jako modalną, czyli najbardziej prawdopodobną, zdaniem eksperta, wartość zmiennej prognozowanej, bądź też jako jej wartość oczekiwaną, a do oceny jej dopuszczalności użyć, odpowiednio, albo określonego przez eksperta prawdopodobieństwa subiektywnego realizacji najbardziej prawdopodobnej wartości zmiennej prognozowanej, albo odchylenia standardowego wariantów prognoz.